Here is a persuasive advertisement for ghostwriting services for the topic of the Weierstrass function:
**Unleash the Power of Mathematical Genius: Expert Ghostwriting Services for Your Weierstrass Function Assignments**
Are you struggling to grasp the intricacies of the Weierstrass function? Do you find it challenging to reconcile its continuous yet nowhere differentiable nature?
Our team of expert ghostwriters specializes in crafting high-quality, plagiarism-free assignments that will leave your professors in awe. With our services, you can:
* Get a deep understanding of the Weierstrass function’s properties and applications
* Produce well-structured, coherent, and mathematically sound essays and papers
* Meet tight deadlines with confidence, without sacrificing quality
Our advantages:
* **Mathematical expertise**: Our writers hold advanced degrees in mathematics and have extensive experience in tackling complex topics like the Weierstrass function.
* **Fast turnaround**: We understand the urgency of academic deadlines and deliver high-quality work quickly, without compromising on quality.
* **Confidentiality**: Our services are completely confidential, ensuring your privacy and academic integrity.
Don’t let the Weierstrass function intimidate you. Let our experts help you unlock its secrets and achieve academic success. Order now and experience the power of mathematical genius!
**Services:**
* Essay writing
* Research paper writing
* Homework help
* Dissertation and thesis writing
* Editing and proofreading
**Order now and get:**
* A well-researched, expertly written assignment that meets your requirements
* A comprehensive understanding of the Weierstrass function and its applications
* A head start on your academic success
Contact us today to discover how our ghostwriting services can help you conquer the Weierstrass function and achieve academic excellence!
### Weierstrass Function
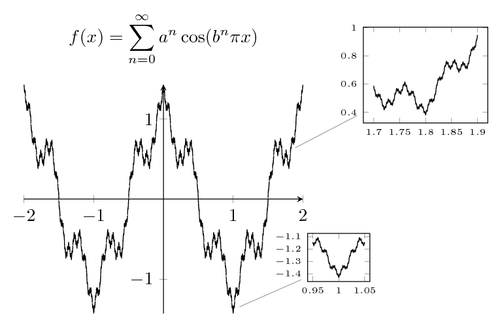
An important application of uniform convergence, and in particular the use of the Weierstrass M-Test, is the following theorem. This theorem states a surprising fact that there exists a continuous function on \(\mathbb{R}\) which is nowhere differentiable. The existence of a continuous function that has no tangent at any point is quite unintuitive. With this property, if you consider the graph of such a function and zoom in at an arbitrary point over and over again, a function will never become smooth or linear. The Weierstrass function is a jagged function known as a fractal curve.
**Theorem 98**.: _There exists a real continuous function on the real line which is nowhere differentiable._
Proof
: For the proof of this theorem we refer the reader to page 154 of [42], where the construction of such a function is explained step by step.
The original Weierstrass function is defined to be
\[f(x)=\sum_{n=0}^{\infty}a^{n}\cos(b^{n}\pi x),\]
where \(0
### Exercises
1. Suppose that the sequence \(\{f_{n}\}\) converges uniformly to \(f\) on the set \(D\) and that for each \(n\in\mathbb{N}\), \(f_{n}\) is bounded on \(D\). Prove that \(f\) is bounded on \(D\).
2. Let \(\{f_{n}\}\) be a sequence of functions with domain \(A\). Show that if \(\sum_{k=1}^{\infty}f_{k}\) is uniformly convergent in \(A\), then \(f_{n}\rightrightarrows 0\) on \(A\).
3. Consider the sequence \(\{f_{n}\}\) defined by \(f_{n}(x)=\frac{nx}{1+nx}\), for \(x\geq 0\).
1. Find \(f(x)=\lim_{n\to\infty}f_{n}(x)\).
2. Show that for \(a>0\), \(\{f_{n}\}\) converges uniformly to \(f\) on \([a,\infty)\).
3. Show that \(\{f_{n}\}\) does not converge uniformly to \(f\) on \([0,\infty)\).
4. Determine whether the sequence \(\{f_{n}\}\) converges uniformly on \(D\).
1. \(f_{n}(x)=\frac{1}{1+(nx-1)^{2}}\)\(D=[0,1]\).
2. \(f_{n}(x)=nx^{n}(1-x)\)\(D=[0,1]\).
3. \(f_{n}(x)=\arctan\left(\frac{2x}{x^{2}+n^{3}}\right)\)\(D=\mathbb{R}\).
5. Suppose a sequence of functions \(\{f_{n}\}\) is defined as \[f_{n}(x)=2x+\frac{x}{n}\)\(x\in[0,1]\).
1. Find the limit function \(f=\lim_{n\to\infty}f_{n}\).
2. Is \(f\) continuous on [0,1]?
3. Does \([\lim_{n\to\infty}f_{n}(x)]^{\prime}=\lim_{n\to\infty}f_{n}^{\prime}(x)\) for \(x\in[0,1]\)?
4. Does \(\int_{0}^{1}\lim_{n\to\infty}f_{n}(x)dx=\lim_{n\to\infty}\int_{0}^{1}f_{n}(x)dx\)?6. Discuss the uniform convergence of the following series:
1. \(\sum_{n=0}^{\infty}\frac{x^{n}}{n!}\) on \(\mathbb{R}\)
2. \(\sum_{n=1}^{\infty}\frac{\sin(nx)}{\sqrt{n}}\) on \([0,2\pi]\)
3. \(\sum_{n=1}^{\infty}\frac{\cos^{2}(nx)}{n^{2}}\) on \(\mathbb{R}\)
7. Let \(f_{n}:[0,1]\to\mathbb{R}\) be a sequence of continuous functions such that
\[\int_{0}^{1}\left(f_{n}(x)-f_{m}(x)\right)^{2}\,dx\to 0\quad\text{as }n,m\to\infty.\]
Let \(k(x,y)\) be a continuous real-valued function on \([0,1]\times[0,1]\). Define
\[g_{n}(x)=\int_{0}^{1}k(x,y)f_{n}(y)\,dy.\]
Prove that the sequence \(\{g_{n}\}\) converges uniformly.
Hint: show that the sequence \(\{g_{n}\}\) is a Cauchy sequence in the sup norm of \(C[0,1]\).
8. Show that there exists a continuous function defined on \(\mathbb{R}\) that is nowhere differentiable by proving the following:
1. Let \(g(x)=|x|\) if \(x\in[-1,1]\). Extend \(g\) to be periodic. Sketch \(g\) and the first few terms of the sum \[f(x)=\sum_{n=1}^{\infty}\left(\frac{3}{4}\right)^{n}g(4^{n}x).\]
2. Use the Weierstrass M-test to show that \(f\) is continuous.
3. Prove that \(f\) is not differentiable at any point.
9. Can we differentiate the series
\[x=\sum_{k=1}^{\infty}\left(\frac{x^{k}}{k}-\frac{x^{k+1}}{k+1}\right),\quad 0 \leq x\leq 1\]
term by term?10. Find an example of a sequence \(\{f_{k}\}\) that converges uniformly to \(0\) on \([0,\infty)\), where each \(\int_{0}^{\infty}f_{k}(x)dx\) exists, but \(\int_{0}^{\infty}f_{k}(x)dx\to\infty\). Does this contradict Theorem 94?
11. Use Dirichlet’s test to show that the trigonometric series \(\sum_{n=1}^{\infty}\dfrac{\text{sin}n\theta}{n}\) converges uniformly to \(\dfrac{\pi-\theta}{2}\) on the interval \([\delta,2\pi-\delta]\) for any \(\delta>0\).
12. Let \(f\) be a continuous function on \(\mathbb{R}\). Let
\[\dfrac{1}{n}\sum_{n=0}^{n-1}f\left(x+\dfrac{k}{n}\right).\]
Show that \(\{f_{n}(x)\) converges uniformly to a limit on every finite interval \([a,b]\).
13. Let \(f_{n}\in C[a,b]\) be a monotone increasing sequence \(f_{1}(x)\leq f_{2}(x)\leq\cdots\) which converges pointwise to \(f(x)\in C[a,b]\). Show that the convergence is uniform on \([a,b]\).
### 2.4 Approximation by Polynomials
The Weierstrass approximation theorem is one of the crowning results of classical analysis. It states that every continuous function on a closed and bounded interval can be approximated uniformly by algebraic polynomials, i.e., by functions of the form
\[P(x)=a_{0}+a_{1}x+a_{2}x^{2}+\cdots+a_{n}x^{n}\,eUnALT\]
where \(n\) is a positive integer and the \(a_{k}\)’s are real numbers. This theorem is a prototype for a large collection of results in approximation theory and there are many different proofs of this theorem. We start by introducing the notion of _separability_.
**Definition 78**.: A metric space \(M\) is called _separable_ if it contains a countable dense subset.
As we defined before, we say \(A\subset M\) is _dense_ if \(\overline{A}=M\). Roughly speaking, a subset \(A\) of a metric space \(M\) is dense if the set \(A\) union its accumulation points equals the metric space \(M\). For example, the set \(\mathbb{R}\) of real numbers is separable since the countable set \(\mathbb{Q}\) is dense in \(\mathbb{R}\). This is so, because as proved in the earlier chapter, every real number can always be given as the limit of a sequence of rational numbers, or, equivalently, because there always exists a rational number arbitrarily close to any given irrational number. There are other examples of separable spaces. These all depend on two facts: the set \(\mathbb{Q}\) of rational numbers is countable and the Cartesian product of any finite number of countable sets is again a countable set. Thus \(\mathbb{R}^{n}\) and \(\mathbb{C}^{n}\) are separable spaces. However, for the special form of the Weierstrass approximation theorem, we first need to ask the following questions:
#### Dense Subsets of \(C[a,b]\)
* Is \(C[a,b]\) separable? Are there any “useful” dense subspaces of \(C[a,b]\)?
* What are the compact subsets of \(C[a,b]\)?
As usual by \(C[a,b]\) we mean the space of real-valued continuous functions defined on \([a,b]\). We supply \(C[a,b]\) with the sup norm
\[||f||_{\infty}=\sup_{x\in[a,b]}|f(x)|.\]
We proved that convergence in \(C[a,b]\) is the same as uniform convergence. Specifically,
\[f_{n}\to f\ \ \text{in}\ C[a,b]\ \Leftrightarrow\ ||f_{n}-f||_{\infty}\to 0\ \Leftrightarrow f_{n}\rightrightarrows f\ \text{on}\,[a,b].\]
To answer these questions we first make the observation that \(C\left[a,b\right]\) and \(C\left[0,1\right]\) are in “some sense” identical. Thus we need only concern with a single choice of the interval \([a,b]\), and \([0,1]\) is often the most convenient.
**Lemma 9**.: _There is a linear isometry from \(C\left[0,1\right]\) onto \(C\left[a,b\right]\) that maps polynomials to polynomials._
Proof
: Define \(g:[a,b]\rightarrow[0,1]\) by
\[g\left(x\right)=\frac{x-a}{b-a}\ \ \ \text{for}\ \ a\leq x\leq b;\]
then \(g\) is a homeomorphism. Note that a homeomorphism is a one-to-one, onto map for which both \(g\) and \(g^{-1}\) are continuous. In mathematics, we think of homeomorphic spaces as being essentially identical.
The map
\[T_{g}:C\left[0,1\right]\to C\left[a,b\right]\]
\[T_{g}\left(f\right)=f\circ g\]
defines a linear isometry from \(C\left[0,1\right]\) onto \(C\left[a,b\right].\) We observe the following about \(T_{g}\):
发表回复